昨今の大学受験数学のトレンドを踏まえ数学の勉強方法を紹介します。
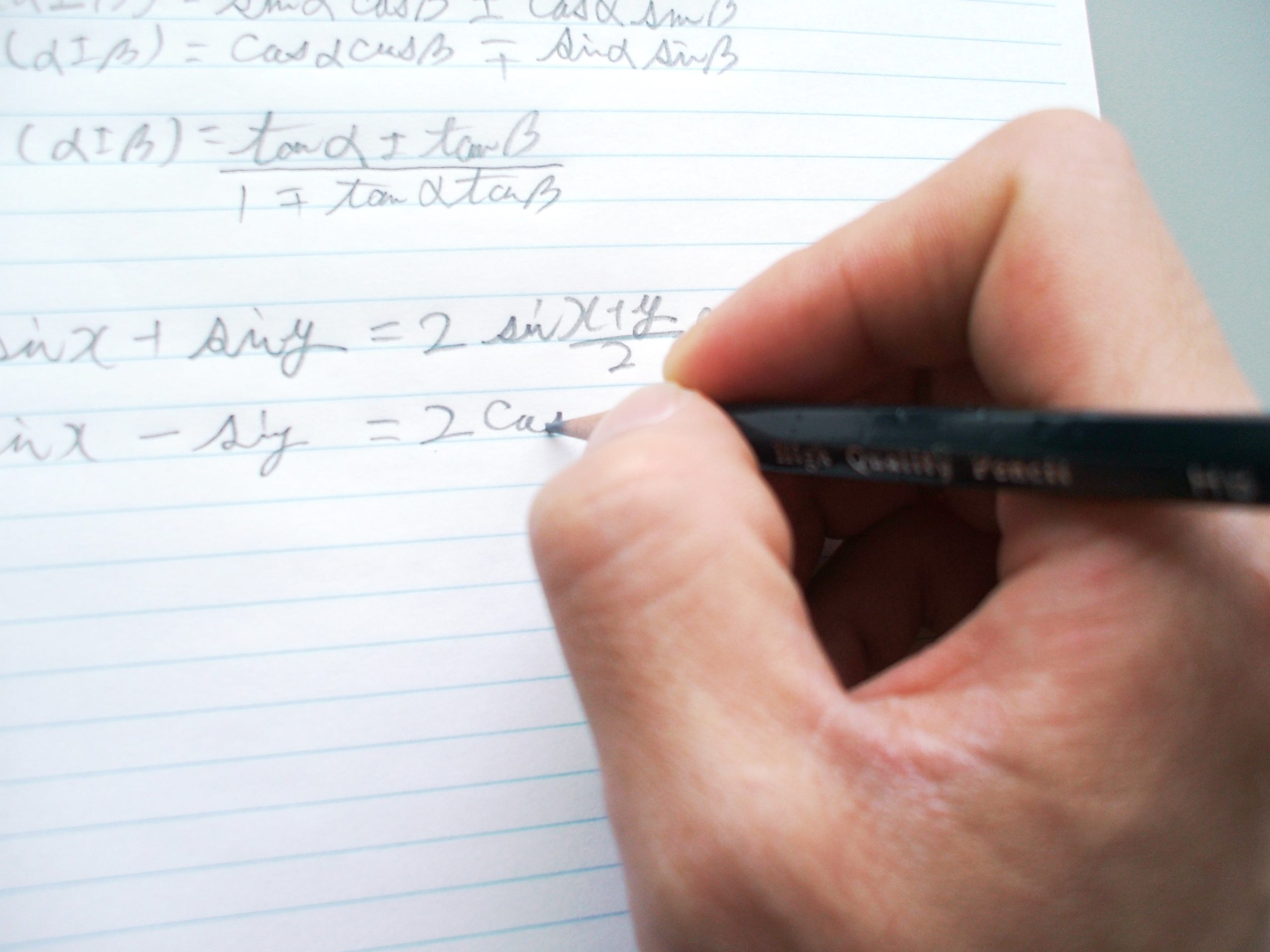
初めに世の中の多くの受験生が抱えている問題として数学は難しい、公式を覚えても問題が解けないなどの点が挙げられますが、基本的に大学受験の数学はいわゆる暗記科目と何ら変わりません。一部の難関大では思考力を問われる問題が出題されますが数学のみのおおよその合格者平均を算出すればその手の問題の得点は限りなく低いことがわかります。
そしてここで挙げた難関大学とは数学のみに焦点を当てれば東大理系、文系(近年)、京大理系、一橋、東工大、早稲田理工、商、慶應理工あたりが該当します。
上記大学を目指される方で高3以上の方は一人一人の能力、進捗により戦略的に勉強を進めなければならないため一般的な突破方法というものがありません。
これらの大学を目指す高校1,2年生や学校の成績を上げたい数学ができるようになりたいという方へのおすすめの方法です。
数学の全般的な勉強方法

1,公式の暗記
当然のことと思われる方も多いと思いますが、指導している側から見ればここが抜けているから問題が解けない、成績が上がらないケースがかなり多いです。
例えば三角関数の加法定理です。公式を覚えている生徒の多くは数学2まで学習が進んでいればsin(α+β)は?と聞かれれば答えることができるでしょう。しかしcosαcosβ-sinαsinβは?と問われれば手が止まる生徒は一気に増えます。また公式を聞かれているという前提条件が無ければさらに正答率は下がります。加えて些細なことと思われるかもしれませんが多くの市販の教科書、参考書には加法定理に使われている文字はαとβです。
これをcosxcosy-sinxsinyこのように問われればさらに正答率は下がります。これがいわゆる公式の逆です。公式を左から右に覚えることができても右から問われれば答えられない、使うことができない。これにより多くの生徒は失点します。特に受験が近い生徒ほどこの点をしっかり行うことが大切になってきます。
2,基本問題の演習

私は数学は暗記科目と変わらないとは述べましたが試験の形式は暗記科目である社会科系科目とは異なります。いくら知識だけあっても多くの数学の問題は計算をしなければ答えは出ません。
そしてこの計算力に関しては個人の能力に依存する部分が大きいので万能な勉強方法はありません。特に計算ミスに関しては個人の性格の部分も大きいです。
しかし受験生の中で一部の特殊な訓練を受けている生徒を除けば計算スピードはさほど変わりません。
解答時間に差のつくところは問題を見たときに解法を思いつく速さです。後に記載しますが難関大の数学を解くうえでここが最も重要になります。
そのため問題を見て解法を考え実際に手を動かす訓練が必要となります。
ここで焦点を当てるのが”解法を考え”の部分です。私が受験数学の問題を解く際、考えて解いている問題はごく一部です。多くの問題はその問題に触れたことがある、類題を解いたことがある、つまり”知っている”から解ける状態になっています。周りにいる数学がよくできる子の多くはこのパターンが非常に多いです。
したがって初めは計算練習も兼ねて問題を解き解いた問題を覚えこむスタンスでやってください。
学年にもよりますがこの段階では教科書併用問題集や青チャートを使うといいでしょう。
(少し突っ込んだ意見を述べれば教科書併用問題集は使うものによりかなり完成度に良し悪しがあります。)
またこの作業をする際に”受験頻出分野”から取り掛かることもとても大切です。こちらも後ほど分野別の勉強の仕方で掲載します。
3,問題のレベルを上げる

1,2を完璧にこなせば某大手予備校の模試を受験すれば基本的に偏差値60を大きく下回ることはなくなると思います。ここからさらに成績を上げるために必要となってくることが知っている問題を増やす、問題のレベルを上げること、記述力を身につけることです。
ここでの勉強方法は基本的に2と同じです。とにかく問題を解きその問題を覚えるまでやりこんでください。問題集の選び方としては書店で解答が一番読みやすい(わかりやすい)ものをおすすめします。
(理由は独学で勉強を進める上で解答解説を読んで理解できないレベルの問題を解いてもわからないところが多すぎて消化することができません。わからない問題も解答を読み理解し覚えていかなければならないからです。)
例を挙げれば標準問題精講1A,2B,3や理系数学のプラチカ1A2Bなど。
またこの段階では一冊に絞りその一冊を完璧に覚えこむことを意識してください。このレベルの問題集は重要な問題は被る上に問題自体が中々難しいので想像以上に時間を要します。またこのようなレベルの問題集の解答をきちんと読むことは自身の記述力向上にも繋がります。高校生からよく耳にする答えは出るのですが~答えはわかるのですが~は本質的に理解できていないケースがほとんどです。
実は数学の問題の中には問題文に書かれている数式たちを闇雲に計算していれば答えが出る問題が多数存在します。
大学受験の記述式の問題の多くは加点法で採点されています。したがってこのような問題が受験で出題され式の羅列のような根拠のない答案を書けば加点に値する部分が少なく、その問題の得点は限りなく低くなります。
私自身も模試の採点を請け負っていたことがありましたが、そのような答案には”部分点”が付けられませんので答えの数値が合っていても限りなく0に近い点数しかつけることができませんでした。
受験を終えた生徒たちの得点開示と実際に書いた答案を再現していただき採点すればおおよそ一致するので受験本番も同様の基準で採点されていることがわかります。
したがって記述がメインとなってくる大学を受験する場合3で解答の書き方も学んでください。
4,志望校対策

ここまでを完璧にこなすことができた子はかなりの力がついていると想像できます。
多くの生徒がここまで到達する頃には3年生になっていると思います。
某大手予備校の模試などを受験すれば偏差値65前後は安定して取ることができるでしょう。
しかしあくまでも目標は難関大…となればこのままでは実力が足りていない生徒がほとんどだと思います。
ここまで来るとどんな知識を入れ、どのように試行できるかは個人の理解力と反復練習の数によって完成度はかなり変わってきます。しかし“数学の勉強の仕方“はしっかり身についていると思います。
したがって一般的には問題のレベルを上げ3と同じことをすればよいと思います。
また避けて通れないことが自分の志望校の赤本を解くことです。どのような問題が出るのかどのような時間配分で問題を解いていけばよいか、いわゆるその大学の傾向を掴む作業です。しかしこの作業は受験生が独学で行うことはかなり難しいです。
理由としては合格していく生徒が2月末の一番完成度が高い時期に受けても難関大の数学のボーダーは5割程度です。この5割というのはあくまでも部分点を含めての5割となります。例えば大門が5つあれば解けた!と思うのは多くても2問程度です。つまり半分以上の問題は答えが出ない、完璧に解けなくても合格するのです。
そのレベルの問題を一般的に11月頃解いても解けた感がなくて当然なのです。
あくまでもこれを前提に過去問演習をしてください。

以上が若年層向けの数学の勉強方法となります。
当塾ではこれらの方針を元にペース作りおよび高校生が自分では手の届かないところに着手させていただきます。
極論を言えば必要なところだけ学習すれば受験では高確率で合格点を取ることができます。
過去問の研究、近年のトレンドの把握、各生徒の能力、進捗状況から必要なところを分析させていただき指導いたします。

