大学受験において、学科選びに悩む方、多いのではないでしょうか。
「志望大学は選びやすいが、学科は具体的に何をやっているのか分からない」
「webサイト等を見ても分かり辛く、調査の手が進まない」
という声を、当塾でも多く聞きます。
そこで当塾のブログでは、現役大学生・大学院生が各学科でどのような事を学べるのか、自身の実体験を元に説明させていただきます!
なるべく高校生の方に親しみやすく感じていただけるよう、高校で身に付ける知識を交えながら説明させていただきますので、よろしければお付き合いくださいませ。
今回は学科紹介の第1弾として、経営工学科について説明させていただきます!
ふわっとした経営工学の説明
まずは本当にふわっと、経営工学についてご説明します!
なのでなんとな~く、経営工学の全体像を把握していただけますと幸いです。
そもそも学問の名前が、「経営工学」ですので、「経営」が関連している学問なのは想像に難くないかと思います。
経営においては、課題に対して意思決定を行うべき場面が多々あります。
例えば「商品を作って、売る会社ならば、利益を最も多く出すためには、商品は何個作るのがよいのか。」という課題。
作る数が多すぎれば、商品が余って無駄に作る分のお金がかかるので得られる利益が減りますし、作る数が少なすぎれば、本来売れるはずの商品を売れず、
本来得られるはずの利益を得られない事があります。
では、どうやって利益が最大になる商品の個数を導き出せるのか。
このような、経営課題に対する答えを、数学の力を借りて、導出する方法論の集合が、経営工学という学問なのです。
大学で登場する、基礎的な想定課題
さて、この段落では、より具体的に経営工学を理解していただくため、
簡単な経営課題例をあげ、それに対する経営工学の知識を用いた解法を説明させていただきます。
課題例を以下にあげてみました。
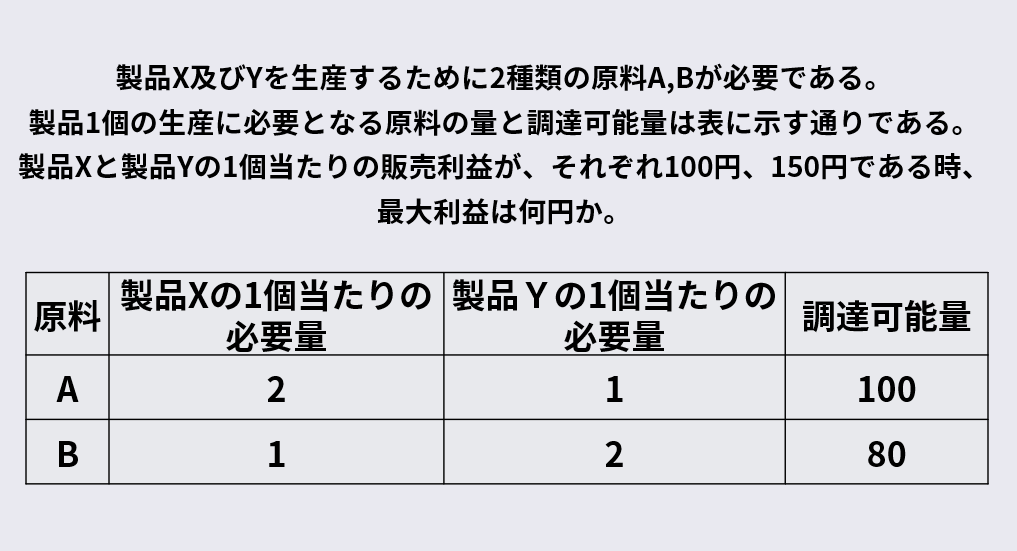
大学では、このような想定課題が登場し、解法を講義で学んでいきます。
今回例にあげた課題は超基礎的な内容で、高校数学の、数学Ⅱの知識を使えば、簡単に解くことが出来ます。
数学Ⅱを学習された方は、一度解を考えてみて下さい。
解法・解答は次の段落でご紹介します。
解法は「線形計画法」
解法を一言で言えば、「線形計画法」なのです。
具体的な解法は以下の通り。
製品Xの精算個数をx、製品Yの精算個数をyとした場合、原料A・原料Bの調達可能量についての制約を、それぞれ次の式のようにあらわすことができます。
・2x + y ≦ 100
・x + 2y ≦ 80
これらを書き換えると、
・y ≦ -2x + 100・・・「式1」とする。
・y ≦ -x/2 + 40・・・「式2」とする。
そして、これら2つの式が示す領域をグラフに落としこむと以下の通り。
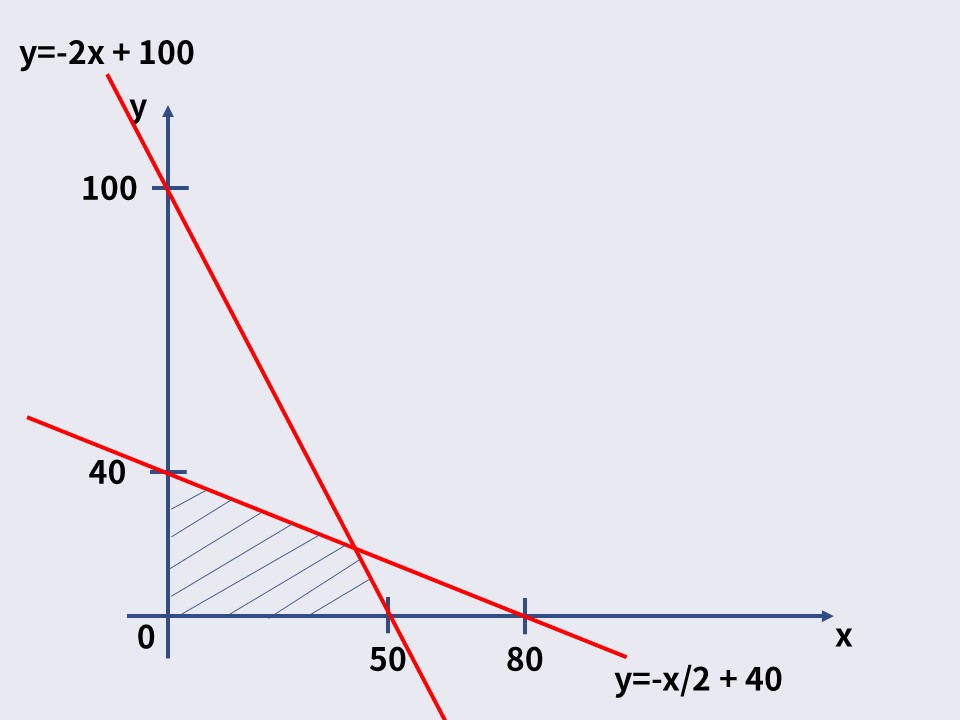
斜線部分が、2つの式が示す領域なわけです。
ちなみに、利益は、xとyを使って、「100x + 150y」と言えます。
よって今回は、斜線領域内において、100x + 150yのとりうる最大値を求めれば、それが課題の答えとなるわけです。
ただし、x,yはそれぞれ「製品数」を示す変数なので、0以上の整数である事を忘れずに。
まず、100x + 150y = zとおきます。
これを書き換えて、
y = -2x/3 + z/150・・・「式3」とする。
zの値を動かしながら、式3の直線をグラフに反映させていきます。
zの値を動かし、それに連動して式3が表す直線を上下に動かしていった結果、
・z/150の値が最大値(つまりzの値が最大値)
・ただし、「式3」の直線が式1と式2が示す領域内を通る
・ただし、x,yの値が0以上の整数
である時、その時のzの値が、今回求めたい、「最大利益」です。
今回は以下の図の通り、最大利益は7000円となります。
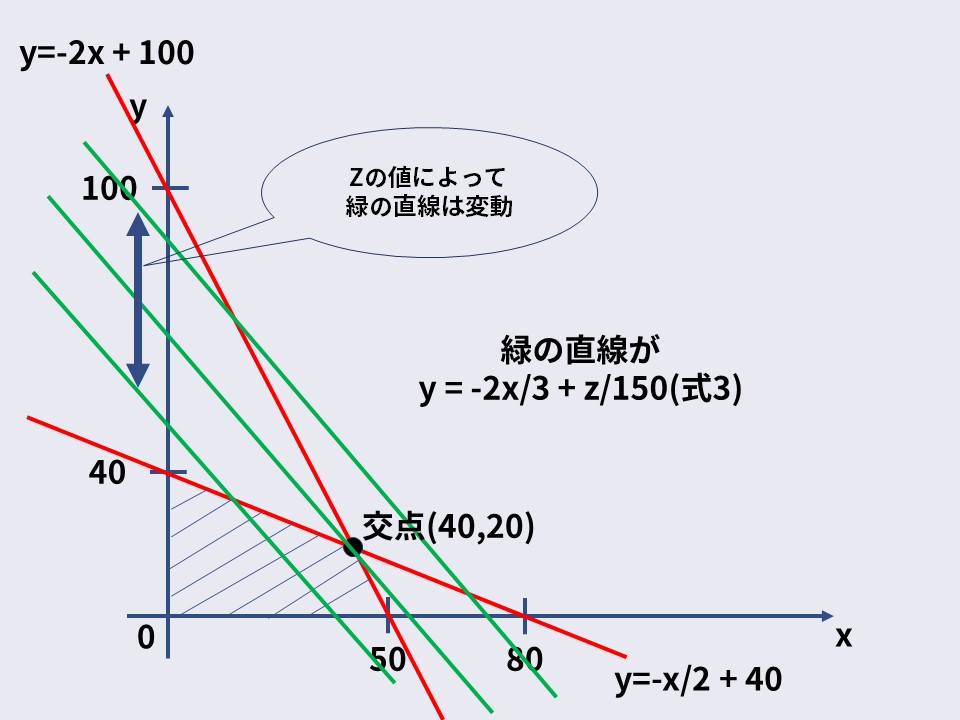
この時のx,yはそれぞれ40,20です。
つまり、xを40個、yを20個生産する時、最も利益が大きくなるという事です。
この学問では、プログラミングも学びます
今回の記事では、手計算で、しかも高校数学の知識で解けるような想定課題をご紹介しましたが、
勿論大学では、より複雑な想定課題を紹介され、その解法を学びます。
特に、課題が複雑になってくると、手計算、つまりは人間の計算力で解を導くのは不可能です。
よって、今流行りのプログラミングや、エクセルのツールが、解を導くためのツールとして登場します。
プログラミングにより、PCに計算をさせ、人間の計算力では解を導き出せないような想定課題に対する解を導くような事を大学では行います。
今回の総括
経営工学は、経営課題を、数式に落としこみ、時にはプログラミングを行う事で解決する方法を学ぶ学問だと言えるでしょう。
ゆえに、プログラミングをやってみたい方、数学が社会で生かされる事を実感したい方、プログラミングを使った経営課題解決の疑似体験をしたい方におすすめの学科と言えます。

